Wstęp

Używanie języka programowania związane jest nieodłącznie z programowaniem. Dosyć trudno znaleźć ładną definicję programowania. Wikipedia jedno niewiele znaczące słowo zastępuje potokiem słów trywializujących zadanie do problemu projektowania, tworzenia, testowania i utrzymywania kodu źródłowego programów komputerowych.
To tak jakby tworzenie muzyki określić jako „ustawianie nut na pięciolinii” 🙂
Angielska Wikipedia programowanie określa jako: a process that leads from an original formulation of a computing problem to executable computer programs. I to chyba jest nieco trafniejsze. Choć zaczyna się od nowego pojęcia computing problem.

Problem obliczeniowy

Zatem co to jest problem obliczeniowy (computing problem)?
Wyobraźmy sobie bardzo proste zadanie: mamy znaleźć miejsca zerowe funkcji \(y=f(x)=ax^2+bx+c\). Oczywiście dla dowolnych wartości \(a,  b\) i \(c\).
Naiwne rozwiązanie jest znane: są dwa miejsca zerowe, a współrzędne wyznacza się ze wzoru:
$$x_{1,2}=\frac{-b \pm\sqrt{b^2-4ac}}{2a}$$
ale po krótkim namyśle zauważamy, że powyższe równanie jest prawdziwe tylko wtedy gdy \(a\ne0\). Zatem nie podaliśmy ogólnego rozwiązania tylko rozwiązanie „szczególne”.
A więc będą nas interesowały takie problemy obliczeniowe, dla których, dla dowolnego zestawu danych wejściowych spełniających założenia wejściowe, potrafimy podać jednoznaczną metodę rozwiązywania. Tak więc podane rozwiązanie jest dobre dla wyjściowego problemu opisanego tak: znaleźć miejsca zerowe funkcji \(f(x)=ax^2+bx+c,\;a\ne0\).
Oczywiście dla oryginalnego problemu można również podać uniwersalne metody jego rozwiązywania, które będą uwzględniały warunki \(a=0,\; b\ne0\) oraz \(a=0,\; b=0\).

Komputer

Z drugiej strony pojawia się „realizator” ogólnego rozwiązania problemu obliczeniowego — komputer. Wszyscy wiedzą, oczywiście, co to jest komputer, a nawet go widują (codziennie). W czym zatem problem?
Żeby problem przybliżyć opowiem jednak co to jest komputer.

Kalkulator

Wyobraźmy sobie najprostszy, czterodziałaniowy komputer. Składa się on (z punktu widzenia użytkownika) z prostej klawiatury oraz czterech klawiszy działań i dodatkowo klawisza „równa się”, którego używamy do zakończenia obliczeń i uzyskania wyniku.
Pozostawiony sam sobie kalkulator nic ciekawego nie wymyśli, ani nie wyświetli na wyświetlaczu żadnego rezultatu (chyba, że jest popsuty ma bogate życie wewnętrzne i sam z siebie coś generuje). Do sensownego jego użycia potrzebny jest operator, który sekwencją naciśnięć klawiszy potrafił będzie z kalkulatora skorzystać.
Kalkulator, na pierwszy rzut oka nie bardzo nadaje się jako przykład działania komputera. Ale — zaufajcie mi, jestem informatykiem — jest to jeden z lepszych przykładów.
kalkulator
Komputer od kalkulatora odróżnia się, że poza rejestrem akumulatora (który jest częścią procesora) posiada znacznie więcej pamięci dodatkowych służących do przechowywania danych, wyników pośrednich oraz rezultatów obliczeń. Kalkulator wymaga jeszcze operatora który wie co chce liczyć i w pamięci (albo na kartce) ma plan (kolejność) działań. Komputer przechowuje tę kolejność w postaci programu i (ciągle jeszcze) potrzebuje człowieka, żeby programy tworzyć.

Przykład „praktyczny”

Wyobraźmy sobie, że do rozwiązania problemu

$$x_{1,2}=\frac{-b \pm\sqrt{b^2-4ac}}{2a}$$
mamy zespół ludzi potrafiący wykonać pojedynczą operację arytmetyczną:

• A potrafi dodawać
• B potrafi odejmować
• C i D potrafią mnożyć
• E potrafi dzielić i wyciągać pierwiastki

Planujemy zatem rozwiązanie problemu, dzieląc zadanie na elementarne operacje

1. \(t_0=-b\),
2. \(t_1=b*b\),
3. \(t_2=2a\),
4. \(t_3=4a\),
5. \(t_4=t_3c\),
6. \(t_5=t_1-t_4\),
7. \(t_6=\sqrt{t_5}\),
8. \(t_7=t_0-t_6\),
9. \(t_8=t_0+t_6\),
10. \(x_1=\frac{t_7}{t_2}\),
11. \(x_2=\frac{t_8}{t_2}\).

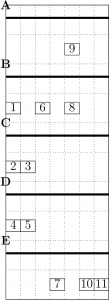
(Nie przejmuję się teraz zadaniami „zdegenerowanymi”, w których krytyczne parametry mają wartość 0.)
Zwracam uwagę, że każda operacje to pojedyncza operacja dwuargumentowa. W istocie procesor tylko takie potrafi wykonywać: pojedyncze operacje na dwu argumentach.
Teraz zadania musimy przydzielić „fachowcom”. Przedstawia to poniższy rysunek.

Zwracam uwagę, że za każdym razem gdy zmieni się zestaw dostępnych fachowców i ich kompetencje — rozdział zadań będzie wyglądał inaczej. W szczególności możemy mieć tylko jednego, uniwersalnego fachowca, który potrafi wykonać każde obliczenia. Wówczas sytuacja będzie wyglądać jeszcze inaczej.
Naszym fachowcem jest uniwersalny procesor. Niestety jego uniwersalność ogranicza się do czterech podstawowych działań arytmetycznych: dodawanie, odejmowanie, mnożenie i dzielenie. Oprócz działań arytmetycznych wykonuje on operacje logiczne (suma logiczna, iloczyn logiczny,…). Dodatkowo potrafi on sprawdzić znak liczby (w układzie dwójkowym znak liczby kodowany jest jako 1 bit — najbardziej znaczący czyli znajdujący się najbardziej po lewej stronie). Zatem wystarczy go sprawdzić. Procesor potrafi jeszcze powiedzieć czy liczba jest równa zeru. Każda kolejna operacja (na przykład sprawdzenie czy A jest większe od B sprowadza się do odjęcia od A B i sprawdzenia jaki jest wynik) musi być rozłożona na elementarne operacji. Wyliczenie pierwiastka kwadratowego czy wartości funkcji sinus jest pewnym wyzwaniem wymagającym wykonania bardzo wielu operacji. Na szczęście najczęściej wykonywane operacje dostarczane są w postaci „funkcji standardowych”.